--- title: Preguntas de Matemáticas del examen UNAM description: Revisa estas 12 preguntas de Matemáticas del examen de admisión de la UNAM con sus respuestas para que puedas seguir practicando. image: https://blog.unitips.mx/hubfs/Contenido_Informativo_Blog/03.23_Preguntas%20matem%C3%A1ticas%20UNAM/preguntas-matematicas-examen-unam.png --- [![Unitips](https://www.unitips.mx/staticfiles/base/images/u_logo_292x166.png)](https://www.unitips.mx/) [![Prueba Gratis Unitips](https://no-cache.hubspot.com/cta/default/3888270/201ea933-c4d7-4f5f-8668-c8fe1dc0dac4.png)](https://cta-redirect.hubspot.com/cta/redirect/3888270/201ea933-c4d7-4f5f-8668-c8fe1dc0dac4) ![Navbar Toggler Open Icon](https://www.unitips.mx/staticfiles/jumpstart_template/assets/img/icons/interface/icon-menu.svg) ![Navbar Toggler Close Icon](https://www.unitips.mx/staticfiles/jumpstart_template/assets/img/icons/interface/icon-x.svg) - [Blog](https://blog.unitips.mx) - Cursos [UNAM](https://www.unitips.mx/cursos-admision/guia-unam/) [UAM](https://www.unitips.mx/cursos-admision/guia-uam/) [IPN](https://www.unitips.mx/cursos-admision/guia-ipn/) [CENEVAL EXANI-II](https://www.unitips.mx/cursos-admision/guia-ceneval/) [EXHCOBA](https://www.unitips.mx/cursos-admision/guia-exhcoba/) [COLLEGE BOARD PAA](https://www.unitips.mx/cursos-admision/guia-college-board-paa/) [COMIPEMS](https://www.unitips.mx/cursos-admision/guia-comipems/) [Todos los cursos](https://www.unitips.mx/cursos-admision/) - [Planes](https://www.unitips.mx/planes-y-precios/) Preparación abril 03 # Preguntas de Matemáticas del examen UNAM ![Unitips](https://blog.unitips.mx/hubfs/new-profile-pic-unitips-blog.png) Unitips ![](https://blog.unitips.mx/hubfs/Promociones/BADGEa-Sep-01-2025-12-34-11-9713-PM.png) ¡Aprovecha los descuentos y arma tu plan a la medida! [Visita Planes](https://www.unitips.mx/planes-y-precios/) [![Nueva llamada a la acción](https://no-cache.hubspot.com/cta/default/3888270/4f2a3eba-3db9-4844-9f49-3b9c05c586de.png)](https://cta-redirect.hubspot.com/cta/redirect/3888270/4f2a3eba-3db9-4844-9f49-3b9c05c586de) [![Nueva llamada a la acción](https://no-cache.hubspot.com/cta/default/3888270/572af1c7-9131-4279-8c55-7210cc637292.png)](https://cta-redirect.hubspot.com/cta/redirect/3888270/572af1c7-9131-4279-8c55-7210cc637292) × ## 12 preguntas de Matemáticas en el examen de admisión UNAM Aunque todas las **secciones del examen de admisión son importantes**, para muchos aspirantes las **preguntas de Matemáticas del examen de la UNAM** requieren mayor atención y horas de estudio. Sigue practicando con el **banco de preguntas con respuesta** que te compartimos a continuación. ## ¿Qué preguntas de Matemáticas vienen en el examen UNAM? La **sección de Matemáticas** es la que contiene el **mayor número de reactivos** en todas las versiones del [temario del examen de la UNAM](https://blog.unitips.mx/la-estructura-del-examen-de-ingreso-la-unam) y suele abarcar de **26 a 24 reactivos**, por lo que es muy importante que todos los **aspirantes le dediquen tiempo suficiente**. Aunque en realidad la UNAM **no establece un número de aciertos mínimos** para el ingreso, la **dificultad para ser seleccionado**, especialmente en las [careras más demandadas](https://blog.unitips.mx/carreras-mas-demandadas-de-la-unam), exige que los aspirantes alcancen el **mayor número de aciertos** posibles. Las **preguntas de Matemáticas de la UNAM** abarcan temas de bachillerato sobre **álgebra, geometría y cálculo**. Sin embargo, para que conozcas más sobre su **estructura y nivel de dificultad**, responde el siguiente **examen diagnóstico** que te ayudará a medir tu nivel de conocimientos. [![Nueva llamada a la acción](https://no-cache.hubspot.com/cta/default/3888270/b897ab87-3cdd-46b7-81fa-dc56af30366a.png)](https://cta-redirect.hubspot.com/cta/redirect/3888270/b897ab87-3cdd-46b7-81fa-dc56af30366a) ## 12 preguntas del examen de admisión UNAM de Matemáticas Una de las mejores estrategias para aprender [cómo estudiar matemáticas](https://blog.unitips.mx/como-mejorar-en-matematicas) es **a través de la práctica constante**. Por eso, a continuación, encontrarás 12 **preguntas del examen UNAM de Matemáticas** que provienen de la guía actualizada de 2023. Cada una viene con una pequeña **retroalimentación que te ayudará a reconocer tus errores** con mayor facilidad. Sin embargo, necesitas contar también con **otro tipo de herramientas de estudio** que te ayuden a reforzar tus conocimientos. Regístrate en el siguiente enlace para obtener acceso al [curso para entrar a la UNAM](https://www.unitips.mx/cursos-admision/guia-unam/) de Unitips, donde encontrarás todo el temario explicado en **lecciones breves y animadas**. [![Nueva llamada a la acción](https://no-cache.hubspot.com/cta/default/3888270/932052a6-7bc5-4553-b1ad-77c5e15bea15.png)](https://cta-redirect.hubspot.com/cta/redirect/3888270/932052a6-7bc5-4553-b1ad-77c5e15bea15) ### Productos notables y factorización 1. ¿Cuál es la factorización del siguiente trinomio x2-11x+30? 1. (x+5)(x+6) 2. (x+1)(x+30) 3. (x-5)(x+6) 4. (x-5)(x-6) Para factorizar un **binomio del tipo x2+bx+c**, se debe encontrar un par de números “m” y “n” tales que la **suma de éstos sea “b” y su producto “c”**. La factorización queda de la siguiente manera: $$x^2+bx+c=(x+m)(x+n)$$ En este ejercicio debemos **encontrar dos números** que, al **sumarse den -11 y al multiplicarse 30**. los únicos que cumplen estas condiciones son -5 y -6: $$(-5)+(6)=-11$$ $$(-5)+(6)=30$$ $$x^2+11x+30=(x-5)(x-6)$$ La respuesta **correcta es el inciso d)**. Factoriza la siguiente expresión: n6-3n3-18 1. (n3 + 3)(n3 – 6) 2. (n3 – 3)(n3 + 6) 3. (n3 – 3)(n3 − 6) 4. (n3 + 3)(n3 + 6) La expresión anterior puede factorizarse como un **trinomio de segundo grado** si aplicamos un **cambio de variable**. 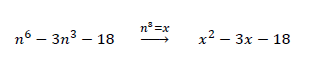Si establecemos que **x = n3**, la expresión puede reescribirse como: ![](https://blog.unitips.mx/hs-fs/hubfs/image-png-Apr-03-2023-08-13-27-6481-PM.png?width=800&height=183&name=image-png-Apr-03-2023-08-13-27-6481-PM.png) La expresión transformada puede factorizarse al encontrar un **par de números que sumados den -3 y multiplicados -18**, estos son 3 y -6: $$x^2-3x-18=(x+3)(x-6)$$ Por último, regresamos a la variable original: ![](https://blog.unitips.mx/hs-fs/hubfs/image-png-Apr-03-2023-08-14-14-4590-PM.png?width=800&height=141&name=image-png-Apr-03-2023-08-14-14-4590-PM.png) 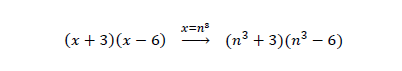La respuesta correcta es el **inciso a)**. 3. Simplifica la siguiente fracción. $$\\frac{x^2+3x-40}{x+8}$$ 1. x – 40 2. x – 5 3. x + 8 4. x – 2 Para **simplificar un cociente de polinomios**, las expresiones del denominador y numerador deberán estar factorizadas. La expresión que está en el numerador es posible factorizarla encontrado un par de n**úmeros que multiplicados den -40 y sumados 3**, estos son 8 y -5: $$\\frac{x^2+3x-40}{x+8}=\\frac{(x+8)(x-5)}{x+8}$$ La expresión x+8 del denominador **no puede factorizarse**, sin embargo, puede simplificarse debido a que **en el numerador tenemos exactamente la misma expresión** en uno de los factores. $$\\frac{(x+8)(x-5)}{x+8}=x-5$$ La respuesta correcta es el **inciso b).** ### Sistemas de ecuaciones 4. Al comprar 3 kg de naranjas y 2 kg de manzanas se pagaron $42.00. Si se compran 1 kg de naranjas y 3 kg de manzanas se pagan $49.00. ¿Cuánto cuesta el kilo de naranjas? 1. $15.00 2. $9.00 3. $8.00 4. $4.00 El problema anterior **se resuelve con un sistema de ecuaciones**. Para establecer este sistema **empezaremos estableciendo las variables**. - x: precio kg de naranjas. - y: precio kg de manzanas. El primer enunciado dice que **3 kg de naranjas más 2 kg** **de manzanas son $42**, lo cual se puede escribir como: $$3x+2y=42$$ El problema también indica que **1 kg de naranjas más 3 kg de manzanas son $49**. Se expresa de la siguiente manera: $$ x+3y=49$$ El sistema queda como la **integración de ambas ecuaciones**: $$3x+2y=42$$ $$ x+3y=49$$ El objetivo es **sumar ambas ecuaciones** y que alguna de las **variables se elimine**. Para encontrar el **valor de *x***, el precio de las naranjas, se elimina la **variable *y***, para ello multiplicamos por (-3) a toda la ecuación de arriba y por (2) a la ecuación de abajo. Esto se conoce como el **método de eliminación**. $$-9x-6y=-126$$ $$2x+6y=98$$ Finalmente, se suman las ecuaciones y **se resuelve la restante**: $$\\frac{+\\begin{matrix}-9x-6y=-126\\\\2x+6y=98\\\\\\end{matrix}}{-7x=-28}$$ $$ x=4$$ Con este desarrollo, se puede afirmar que la respuesta correcta es el **inciso d)**. 5. A partir del siguiente sistema de ecuaciones, obtén el valor de *x*. 5x-4y=19 7x+3y=18 x=-3 x=-1 x=1 x=3 El **inciso d) es la respuesta correcta**. Para comprobarlo, hay que resolver este [sistema de ecuaciones de dos incógnitas](https://blog.unitips.mx/solucion-de-ecuaciones-con-dos-incognitas), también se usará el **método de eliminación**. Para esto, se eliminará *y* al **multiplicar 3 a la ecuación de arriba y por 4 a la de abajo**. $$15x-12y=57$$ $$28x+12y=72$$ Se suman ambas ecuaciones y se resuelve: $$\\frac{+\\begin{matrix}15x-12y=57\\\\28x+12y=72\\\\\\end{matrix}}{43x=129}$$ $$ x=\\frac{129}{43}=3$$ 6. Soluciona el siguiente sistema de ecuaciones: 5x + 2y – z = –7 x – 2y + 2z = 0 3y + z = 17 1. x = –2, y = 3, z = 5 2. x = 2, y = 4, z = –5 3. x = –2, y = 4, z = 5 4. x = 2, y = 3, z = –5 Primero, **hay que eliminar la *x***, que es la única variable que no se encuentra en la tercera ecuación. Para esto, s**e multiplicará por -5** la segunda ecuación: $$\\frac{+\\begin{matrix}5x\\ +\\ 2y\\ -\\ z=\\ -7\\\\-5x\\ +\\ 10y\\ -\\ 10z=0\\\\\\end{matrix}}{12y-11z=-7}$$ La ecuación obtenida **se agrupa con la última ecuación** del sistema original para tener un **sistema 2x2**, este sistema también puede ser resuelto con el **método de eliminación**: $$3y+z=17$$ $$12y-11z=-7$$ Para obtener el **valor de una de las variables**, hay que multiplicar por 11 la ecuación de arriba y, en seguida, sumarlas. $$\\begin{matrix}(11)(3y+z=17)\\\\12y-11z=-7\\\\\\end{matrix}$$ $$\\frac{+\\begin{matrix}33y+11z=187\\\\12y-11z=-7\\\\\\end{matrix}}{45y=180}\\frac{+\\begin{matrix}33y+11z=187\\\\12y-11z=-7\\\\\\end{matrix}}{45y=180}$$ $$ y=\\frac{180}{45}=4$$ Una vez que **conoces las dos variables**, se elige alguna de las ecuaciones que contenga a la **variable restante**. En este caso, se utilizará la ecuación número dos debido a que *x* **tiene el coeficiente más bajo**. Los valores que satisfacen al **sistema son x=-2, y=4, z=5**. La **respuesta correcta es el c)**. ### Trigonometría 7. ¿A cuántos grados equivalen 11π/18 radianes? 1. 220° 2. 110° 3. 169° 4. 198° Realizar [conversiones de ángulos de radianes a grados](https://blog.unitips.mx/contenido-de-examen-unam-radianes-grados) es sencillo, ya que se cumple con una **variación proporcional directa**, es decir, se puede utilizar una regla de 3, tomando en cuenta que **π radianes = 180°**. $$ \\pi\\ radianes\\ \\ \\ \\rightarrow\\ \\ \\ 180°$$ $$\\frac{11\\pi}{18}radianes\\ \\ \\rightarrow\\ \\ \\ x$$ Se multiplican los entremos y se divide entre π: $$11π18radianes×180°π radianes =110°$$ El **inciso b)** es la respuesta correcta. 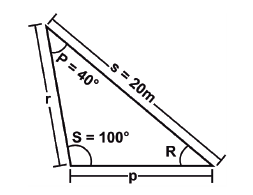8. Determina el valor del lado *p* del siguiente triángulo. Considera: | Sen (40°) | 0.64 | | --- | --- | | Sen (100°) | 0.98 | | Cos (40°) | 0.76 | | Cos (100°) | 0.17 | ![preguntas-matematicas-1](https://blog.unitips.mx/hs-fs/hubfs/Contenido_Informativo_Blog/03.23_Preguntas%20matem%C3%A1ticas%20UNAM/preguntas-matematicas-1.png?width=800&height=617&name=preguntas-matematicas-1.png) 1. 10 m 2. 06 m 3. 34 m 4. 64 m Los **triángulos oblicuos**, es decir, aquellos que poseen un **ángulo mayor que 90°**, se resuelven utilizando la **ley del seno o la del coseno** según los datos que tengamos sobre dicho triángulo. En esta **pregunta de Matemáticas del examen UNAM** se puede relacionar a **uno de sus lados con su ángulo opuesto** (lado s con el ángulo S, ambos conocidos) y al lado que desconocemos con su **ángulo opuesto conocido** (lado p con ángulo P), es decir, es posible **utilizar la ley de senos**. $$\\frac{p}{sen(P)}=\\frac{s}{sen(S)}$$ $$psen(40°)=20 msen(100°)$$ Se colocan los **valores respectivos** de sen (40°) y de sen (100°): $$\\frac{p}{0.64}=\\frac{20\\ m}{0.98}$$ $$ p=\\frac{20\\ m\\ast0.64}{0.98}=13.06\\ m$$ Tras este procedimiento, sabemos que la **respuesta correcta es el inciso a)**. ### Circunferencia, parábola, hipérbole y elipse 9. Determina el centro y el radio de la circunferencia a partir de su ecuación. $${(x+4)}^2+{(y-6)}^2=49$$ 1. C (–4, 6); r = 7 2. C (4, –6); r = 7 3. C (–4, 6); r = 49 4. C (4, –6); r = 49 La [ecuación simétrica de una circunferencia](https://blog.unitips.mx/ecuacion-de-la-circunferencia-guia-de-examen-uam) nos brinda información explícita sobre su **centro y radio**. $$\\left(x-h\\right)^2+\\left(y-k\\right)^2=r^2$$ Las **coordenadas del centro** son C(h,k). Al extraer estos valores de la ecuación de este ejercicio y cambiarles el signo, **se sabe que el centro está en C (-4, 6)**. Por otro lado, el **radio al cuadrado es 49**, para conocer el radio le sacamos la raíz cuadrada, **resultando es r=7**. 10. La ecuación de la parábola cuyo eje focal es el eje y, con el parámetro p = –5 y vértice en el origen es: 1. x2 – 20x = 0 2. y2 – 20x = 0 3. y2 + 20x = 0 4. x2 + 20y = 0 La parábola descrita en este problema es una **vertical con vértice en el origen**, que se deduce a partir de que **el eje *y* es el eje focal** que también es el **eje de simetría de la parábola**. La ecuación simétrica que le corresponde es: $$\\left(x-h\\right)^2=4p(y-k)$$ Como su vértice es el origen, **h y k son 0 respectivamente**, se sustituye el valor de p y terminamos **igualando la ecuación a 0**. $$\\left(x-0\\right)^2=4(-5)(y-0)$$ $$x^2=-20y$$ $$x^2+20y=0$$ La respuesta correcta es el **inciso d)**. 11. Determina el centro de una elipse a partir de la siguiente ecuación: $$\\frac=\\sqrt{45}$$ Con **el centro y los parámetros a y b**, se puede escribir completa la ecuación simétrica: $$\\frac{y^2}{9^2}-\\frac{x^2}{\\left(\\sqrt{45}\\right)^2}=1$$ $$\\frac{y^2}{81}-\\frac{x^2}{45}=1$$ Aunque la anterior ya es la respuesta, sin embargo, **no aparece entre las opciones**. Para obtener el inciso correcto, es necesario **desarrollar algebraicamente** la ecuación. Para esto, se **multiplicará toda la ecuación por el mínimo común múltiplo** de los denominadores, en este casi, 405. $$\\left(405\\right)\\left(\\frac{y^2}{81}-\\frac{x^2}{45}=1\\right)$$ $$5y^2-9x^2=405$$ La respuesta correcta es **el inciso b)**. No olvides que el examen de admisión se encuentra compuesto por un **total de 120 preguntas** y que cada acierto cuenta para lograr tu ingreso. **No descuides las otras materias** y practica con ayuda de [simuladores de ingreso para la UNAM](https://blog.unitips.mx/examen-diagnostico-gratis-de-ingreso-unam) que te permitan **recrear las condiciones de tu examen**. ## Accede a más preguntas de Matemáticas para tu examen UNAM Las **preguntas de Matemáticas** que forman parte del **examen de admisión a la UNAM** constituyen una de las partes más complicadas de esta evaluación, no sólo por la **cantidad de reactivos, sino también por la dificultad** para responderlos. Estudiar y **practicar te ayudará a mejorar**. Además, toma en cuenta el resto de las **secciones que integran tu evaluación**. Asegúrate de contar con el **material adecuado** que te ayude a abarcar todos los temas de una manera efectiva y que **evita que te aburras**. En el siguiente enlace encontrarás acceso a la **versión gratuita del curso en línea** Unitips. Gracias a la [metodología bite-sized learning](https://blog.unitips.mx/microaprendizaje-bite-sized-learning), podrás estudiar todos los temas de tu examen por medio de **clases animadas y breves**, enfocadas sólo en lo que sí te van a preguntar. Regístrate y **recibe tres clases** sin costo: [«Accede a recursos de estudio para todas las materias antes de tu examen de la UNAM. Haz clic aquí e inicia gratis.»](https://bit.ly/33nUUIM) ### Comentarios sobre el blog: Preguntas de Matemáticas del examen UNAM ## Otros Artículos que te podrían interesar ## Aciertos para entrar al IPN ¿Cuántos aciertos se necesitan para entrar al IPN? Conocer los aciertos para est... [Leer publicación](https://blog.unitips.mx/aciertos-para-entrar-al-ipn) Admisiones enero 13 ## Convocatoria UNAM 2026: fechas clave y registro para el ingreso Proceso de ingreso a la UNAM: convocatoria 2026 ¿Planeas formar parte de la Máxi... [Leer publicación](https://blog.unitips.mx/convocatoria-unam) Admisiones enero 22 ## Convocatoria ECOEMS 2026 Asignación al bachillerato 2026: proceso ECOEMS El Espacio de Coordinación de la... [Leer publicación](https://blog.unitips.mx/convocatoria-de-ingreso-a-bachillerato) Admisiones diciembre 19 Unitips hace la diferencia Los aspirantes que estudian con Unitips, tienen resultados por arriba del promedio nacional lo cual hace la diferencia para lograr quedar en la institución de preferencia. #### 5X Aumenta 5 veces tus posibilidades de ingreso a las mejores universidades. #### 43% Alcanza calificaciones 43% arriba del promedio nacional. #### 85% Tus resultados en el examen de simulación predicen hasta en un 85% tus resultados. ##### Cursos - [UNAM](https://unitips.mx/cursos-admision/guia-unam/) - [UAM](https://unitips.mx/cursos-admision/guia-uam/) - [IPN](https://unitips.mx/cursos-admision/guia-ipn/) - [CENEVAL EXANI-II](https://unitips.mx/cursos-admision/guia-ceneval/) - [EXHCOBA](https://unitips.mx/cursos-admision/guia-exhcoba/) - [COLLEGE BOARD PAA](https://unitips.mx/cursos-admision/guia-college-board-paa/) - [COMIPEMS](https://unitips.mx/cursos-admision/guia-comipems/) ##### Empresa - [Unitips](https://www.unitips.mx/) - [Blog](https://blog.unitips.mx) - [Unitips Chile](https://www.unitips.cl/) - [Blog Chile](https://blog.unitips.cl) - [Contacto](https://info.unitips.mx/contacto) - [Centro de ayuda](https://ayuda.unitips.mx) - [Terminos y condiciones](https://www.unitips.mx/legal/terminos-y-condiciones/) - [Aviso de privacidad](https://www.unitips.mx/legal/aviso-de-privacidad/) ![Garantía de satisfacción en nuestros cursos de admisión a Universidad y Bachillerato](https://www.unitips.mx/staticfiles/base/images/medal_garantia.svg) En Unitips queremos que estés contento, así que recuerda que puedes probar el curso completamente gratis UNAM, CENEVAL, UAM, IPN, COMIPEMS, EXHCOBA y COLLEGEBOARD son empresas registradas no vinculadas a Unitips. Este sitio web no esta aprobado ni vinculado a ninguna de estas instituciones. Ninguno de nuestros cursos garantizan el ingreso ni la absoluta similitud en contenidos. El Usuario deberá leer detenidamente las siguientes Condiciones de uso antes de utilizar el sitio web unitips.mx (Sitio Web) y los materiales y contenidos alojados en él. Unitips no garantiza de ninguna manera el ingreso a ninguna institución de educación y se reserva el derecho de cambiar el material de acuerdo a los distintos requerimientos de la empresa. Al ingresar, todos los usuarios están aceptando el aviso de privacidad y los términos y condiciones del sitio. --- © 2021 Unitips Sapi de CV Aviso de privacidad y Terminos y condiciones de uso - - - - - - [mailto:soporte@unitips.mx](mailto:soporte@unitips.mx) ```json { "@context" : "http://schema.org", "@type" : "Article", "about" : [ "", "Universidades en México", "Procesos de Ingreso a la Universidad y Bachillerato" ], "author" : { "@type" : "Person", "name" : "Unitips", "url" : "https://www.unitips.mx/" }, "dateModified" : "abril 03", "datePublished" : "2023-04-03 20:25:38", "description" : "Revisa estas 12 preguntas de Matemáticas del examen de admisión de la UNAM con sus respuestas para que puedas seguir practicando.", "headline" : "Preguntas de Matemáticas del examen UNAM", "image" : { "@type" : "ImageObject", "height" : 400, "url" : "https://3888270.fs1.hubspotusercontent-na1.net/hubfs/3888270/Contenido_Informativo_Blog/03.23_Preguntas%20matem%C3%A1ticas%20UNAM/preguntas-matematicas-examen-unam.png", "width" : 1200 }, "mainEntityOfPage" : "https://blog.unitips.mx/preguntas-matematicas-examen-unam", "publisher" : { "@type" : "Organization", "logo" : { "@type" : "ImageObject", "height" : 60, "url" : "https://blog.unitips.mx/hubfs/base_files_icons/logo-bar-structured-data.png", "width" : 600 }, "name" : "Unitips" } } ```