Solución de ecuaciones con dos incógnitas
¿Te estás preparando para tu examen de admisión y las matemáticas te están dando batallas? ¡No te preocupes! Te preparamos este blog donde te ayudaremos a dominar uno de los temas más importantes del temario de ingreso. Sigue leyendo porque te explicaremos paso a paso cómo resolver los sistemas de dos ecuaciones con dos incógnitas con el mejor sistema.
¿Ya sabes qué tienes que hacer para ingresar a la universidad?
Sistemas de ecuaciones lineales
Como seguro ya habrás visto, este tema forma parte fundamental de los exámenes de admisión, ya que es base de los conocimientos de álgebra que necesitas para ingresar a la universidad. Por eso es importante que lo domines a la perfección.
Aquí utilizaremos el método de reducción, que consiste en sumar o restar las ecuaciones del sistema para eliminar una de las incógnitas.
¿Cómo resolver ecuaciones de dos incógnitas?
Es muy importante saber que se necesitan dos ecuaciones para resolver una ecuación de dos incógnitas. Es por esto que siempre que te pidan resolver este tipo de operaciones, te brindarán dos ecuaciones.
Para desarrollar este proceso, utilizaremos el siguiente sistema de ecuaciones.
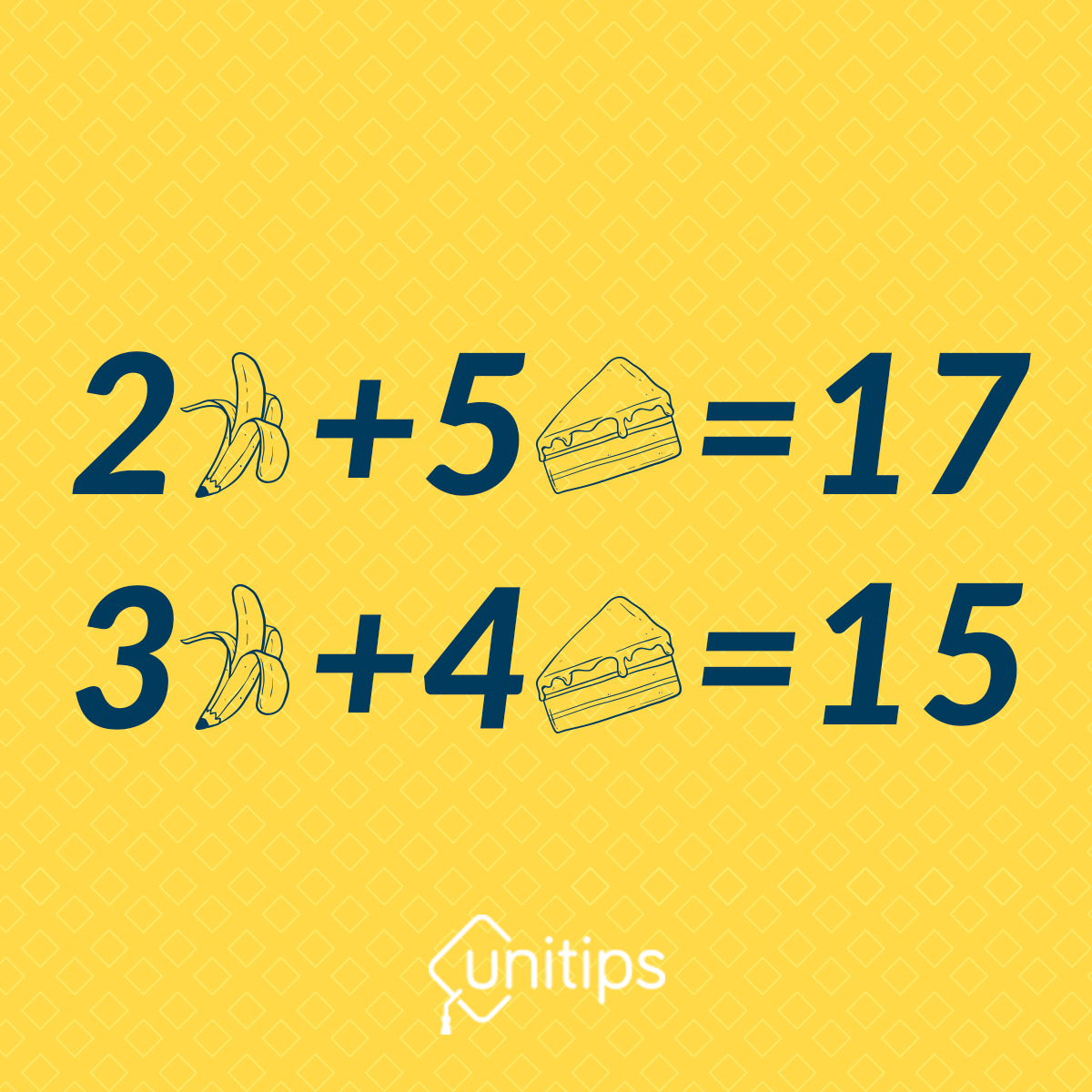Para resolverlo, tomaremos a la 🍌 como x, mientras que 🍰 será reemplazado por y, de modo que quedará así:
Paso 1
Multiplica la ecuación de arriba por el número que está junto a la x con el signo contrario. También multiplica la ecuación de abajo por el número que se encuentra junto a la x, pero sin cambiar el signo.
Fíjate en el ejemplo:
Al realizar la multiplicación, obtenemos este resultado:
Paso 2
Suma o resta (según sea el caso) las x con las x, las y con las y, y los números que no tengan letras.
Escribe el resultado debajo de cada pareja, de la siguiente forma:
Como la x está multiplicada por un cero, se puede eliminar para que sólo te quede una ecuación con una incógnita muy fácil de resolver.
Paso 3
Resuelve la ecuación obtenida en el Paso 2, “pasando” el -7 del otro lado, de modo que aparezca como una división (recuerda no cambiar el signo del -7).
Solamente realiza la división y listo, obtendrás el valor de y.
Paso 4
Ya nada más nos falta conocer el valor de x. Para conocerlo realizamos los mismos pasos, solo que, en vez de tomar los números que están junto a la x, tomamos los que están junto a la y.
Multiplicamos por los números que están junto a la y y cambiamos el signo del que multiplica a la ecuación de arriba.
Lo que nos da:
Ahora sumamos o restamos según el caso:
Eliminamos la y, ya que esta se encuentra multiplicando por 0.
Resolvemos la ecuación “pasando” el 7 como dividendo:
Solucionamos la división y obtenemos el valor de x
¡Listo! Terminamos el ejercicio, la solución es x=1 y y=3.
Por lo tanto, los valores de 🍌 es 1 y de 🍰 será 3.
NOTA: Como seguramente notaste, después de sumar o restar, queda una incógnita que se multiplica por 0 que podemos eliminar. Si no sucede esto, hay algo mal en tus pasos y debes revisar.
Sigue poniendo a prueba tus aprendizajes de este tema y accede al examen diagnóstico gratuito que tenemos a continuación para ti.
¿Qué te pareció? Recuerda que lo más importante para reforzar tus conocimientos es que practiques lo que acabas de aprender con distintos ejercicios, por eso aquí te dejamos una pregunta tipo examen que te ayudará a repasar el contenido de este blog.
Encuentra el valor de las incógnitas en el siguiente sistema:
a) x=2, y=4
b) x=1/2, y=1/4
c) x=-1/4, y=1/2
d) x=1/4, y=-1/2
Solución: x=-1/4, y=1/2
Ya sabemos que te estás volviendo súper pro de los sistemas de ecuaciones con dos incógnitas, pero tu examen de admisión tratará más temas, por lo que revisar más material y obtener otros recursos de estudio, será lo ideal para sacar la mejor calificación posible.
A continuación, te dejaremos un enlace gratuito a la prueba gratuita de Unitips. Aquí encontrarás todas las herramientas para tu examen de admisión a la universidad.
Aumenta tus calificaciones hasta 43%. Regístrate y sigue estudiando sin costo.