Fórmulas de Física que necesitas para tu examen de admisión
Los reactivos de la materia de Física suelen ser una parte importante del examen de admisión y, por lo regular, una de las secciones que más retadora es para los aspirantes. Para ayudarte, aquí te presentamos diez fórmulas de Física que te harán más fácil su estudio.
10 fórmulas de Física que necesitas para tu examen de admisión.
Entre las principales dificultades al resolver un problema de Física está saber qué fórmula aplicar y cómo desarrollarla. Aunque se pueden utilizar varios métodos para obtener un resultado, es mejor utilizar la fórmula adecuada para llegar a la respuesta correcta.
Trabajar de una manera breve y meticulosa podrá ahorrarte tiempo al contestar tu examen de admisión y así dedicarte a otras áreas que te requieran más atención.
Además de conocer y entender estas fórmulas de Física, practicar con ejercicios y preguntas tipo examen te ayudará a mejorar tus habilidades. Realiza el siguiente diagnóstico gratuito del curso Unitips y conoce cuál es tu nivel académico.
¿Cómo hacer tu formulario para Física del examen de admisión?
Una herramienta para estudiar eficiente para cualquier examen es un formulario, que te permitirá sintetizar todos los temas y revisarlos cuando lo consideres necesario.
Puedes hacerlo en una hoja blanca o en computadora. Sin embargo, aquí te preparamos un compilado de todas las fórmulas de Física que revisaremos para que puedas imprimirlo y llevarlo a todos lados.
Descarga aquí tu formulario de Física gratis
1. Distancia.
La fórmula de distancia y tiempo es una de las más importantes pues no sólo viene en la mayoría de los temarios para entrar a la universidad, sino que una sola ecuación te ayudará a saber cualquiera de los tres elementos que te pidan resolver:
En esta, V es Velocidad y T simboliza tiempo. Resolvamos un pequeño ejemplo:
Calcula la distancia de un automóvil que viaja a 70 km/h durante un tiempo de 3 horas.
Lo primero que debes hacer es reconocer qué elemento corresponde a cada parte de la fórmula y sustituirlos.
$$D=V\ \times\ T$$
Deberás cancelar las unidades repetidas que aparecen en el numerador y denominador (en este caso h que determina las horas) y así obtener el resultado:
$$D=V\ (70km/h)\ \times\ T\ (3h)$$
Un truco que puedes usar para despejar los otros valores de la ecuación, es reordenar el siguiente triángulo de operaciones y reordenar los elementos.
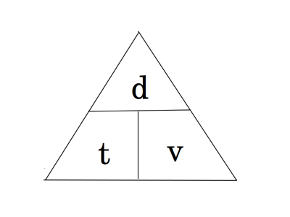Aquí te dejamos un ejemplo:
$$D=210\ km$$
Averigua el tiempo que tarda un avión en llegar de la ciudad Chihuahua a la ciudad de México si la velocidad promedio del avión es de 600 km/h y la distancia entre ambas ciudades es de 900 km.
Para encontrar la solución, deberás dividir la distancia entre el tiempo y cancelar las unidades dobles:
$$T=\frac{D\ (900\ km)}{V\ (600\frac{km}{h})}$$
$$T=1.5\ h$$
Para convertir los números enteros a minutos debes multiplicar el primero por 60. El resultado será 90 minutos y es más probable que el resultado aparezca en esta forma.
2. Aceleración
En la mecánica clásica, aceleración es definida como la variación de la velocidad de un cuerpo por unidad de tiempo.
$$Aceleración=(Cambio de velocidad)/(Intervalo de tiempo)$$
$$a=\frac{V_f-V_i}{D}$$
Donde Dt denota el tiempo transcurrido entre las mediciones de la velocidad Vi y Vf.
En el siguiente ejemplo, te mostramos su aplicación:
Una motocicleta que se mueve con aceleración uniforme, de una rapidez inicial de 4 m/s a una final 10m/s. Si este incremento ocurrió en un lapso de 6s, ¿cuál es la aceleración de la motocicleta?$$a=\frac{10m/s-4m/s}{6s}$$
Realizando la resta y dividiendo conforme a la jerarquía de operaciones, el resultado es 1 m/s².
3. Caída libre
Para estas alturas, seguramente ya sabes que que existe un valor constante para la aceleración de la gravedad que a nivel del mar es:
g = 9.80 m/s².
Por lo tanto, la caída libre no es más que un movimiento rectilíneo uniformemente acelerado (MRUA) y se aplica las mismas fórmulas del movimiento para describirla. Sin embargo, esta cambia de acuerdo con los valores que se conocen. Las formas son estas:
1.
$$y=\frac{V_f+V_0}{2}t$$
2.
$$V_f=V_0+gt$$
3.
$$y=v_0t+\frac{1}{2}gt^2$$
4.
$$y=v_ft-\frac{1}{2}gt^2$$
5.
$$2gy=v_f^2-v_0^2$$
Para todas estas formas, los valores son los siguientes:
- h: es la altura final del objeto.
- y: es la altura inicial del objeto.
- v0: es la velocidad inicial del objeto.
- t: el tiempo transcurrido desde que se lanza el objeto hasta que se mide.
Resolveremos un ejemplo a continuación:
Una pelota de hule se deja caer del reposo. ¿Cuál será su velocidad después de 4 segundos?
Para esto, primero ubicaremos los valores con los que contamos. En este caso, es:
- V0= 0
- g= 9.80 m/s2
- t= 4 s
Gracias a esto, sabemos que tendremos que encontrar la Vf y no existe la altura inicial, por lo que usaremos la forma 2. Sustituimos los valores en la fórmula y resolvemos las operaciones correspondientes:
$$V_f=0+\left(9.80\frac{m}{s^2}\right)\left(4s\right)$$
$$V_f=0+\left(9.80\frac{m}{s^2}\right)\left(4s\right)$$
Las fórmulas de Física pueden llegar a ser demasiada información, especialmente si las estudias solamente con ejemplos y ejercicios. Por eso, te recomendamos que te registres a la prueba gratuita de la plataforma Unitips en línea. Aquí encontrarás videos breves, clases con los mejores profes de México, trivias tipo examen y exámenes de simulación.
4. Prensa hidráulica
De acuerdo con el principio de Pascal, la presión dentro de un fluido hidrostático se distribuye de manera uniforme, esto es, la presión en los extremos de los cilindros de una prensa hidráulica debe ser la misma:
$$\frac{F_1}{A_1}=\frac{F_2}{A_2}$$
Donde en la última expresión hemos utilizado la definición de presión P=FA para cada cilindro en su respectivo émbolo. Revisa el siguiente ejercicios:
Calcula la fuerza que se necesita aplicar en una prensa hidráulica a un émbolo de área 10m² para levantar un peso de 50 N, si el área del segundo émbolo es de 4m².
Se despeja F1 de la fórmula de la prensa hidráulica:
$$F_1=\frac{4m^250\ N}{{10m}^2}$$
Para obtener el valor final, no olvides eliminar los términos semejantes. De este modo, la respuesta es:
$$F_1=20N$$
5. Trabajo y fuerza
El trabajo en física es un concepto ligado al concepto de energía. Esta cantidad se expresa en Joules que representan una unidad de energía. Se define el trabajo (W) efectuado por una fuerza constante (F) como el producto de dicha fuerza actuando sobre un cuerpo que se desplaza una distancia (D).
$$W=F\times D$$
Checa el siguiente ejemplo:
¿Cuánto trabajo se efectúa al dejar caer una caja cuya masa (m) es de 10kg desde una altura (h) de 10 metros?
La fuerza empleada es la fuerza de gravedad que actúa sobre el objeto. Recordemos que ésta se obtiene mediante otra fórmula:
$$F=mg$$
Donde g es la constante de la aceleración de la gravedad. La fuerza actuando sobre la caja será entonces F=(10kg)(9.8m/s²), así F = 98 N. Sustituimos esta fuerza en la fórmula para el trabajo y obtenemos lo siguiente:
$$W=98N\times10m$$
De este modo, tenemos que el resultado es:
$$W=980\ J$$
6. Conversión de Fahrenheit a Celsius
Existen dos escalas de temperatura ampliamente utilizadas en Física, las cuales están relacionadas mediante la siguiente fórmula:
$$°F=°C×1.8+32$$
Resolvamos un ejercicio:
La temperatura reportada por un termómetro en escala Fahrenheit es de 50 °F. ¿Cuál será el valor de la temperatura reportada en escala Celsius?
Podemos efectuar un simple despeje de la cantidad C de la ecuación anterior y obtener:
C = (F - 32) / 1.8
A partir de esta fórmula podemos sustituir el valor de la temperatura en Fahrenheit y obtener el equivalente en escala Celsius.
C = (50 - 32) / 1.8
C = 18 / 1.8
Ahora sabemos que el resultado: C = 10 Celsius
7. Ley de los Gases
Existen varias formulaciones y relaciones entre los gases ideales, Ley de Boyle-Mariotte, Ley de Gay Lussac y Ley de Charles. Estas leyes dependen del tipo de proceso al que se somete un gas, sin embargo, existe una fórmula en Física que contiene todas estas relaciones:
$$(P_1\ V_1)/T_1\ =(P_2\ V_2)/T_2\ $$
Primero, debemos identificar qué tipo de proceso se desea efectuar. Si se trata de un proceso isotérmico, este es un proceso a temperatura constante, es decir, que la temperatura inicial y la temperatura final son la misma: T1=T2. De esta manera la relación entre gases ideales ya no dependerá de la temperatura y la fórmula que describe su comportamiento será:
$$P_1×V_1=P_2×V_2$$
Esta última ecuación corresponde a la Ley de Boyle-Mariotte. A continuación, revisaremos un ejemplo:
Calcula el volumen final de un globo sometido a un proceso isotérmico que inicialmente tiene un volumen de 10 L, que cuya presión se incrementa al doble de la presión inicial.
En este problema no necesitas conocer el valor exacto de la presión inicial, únicamente basta con saber el cambio relativo de la presión. Veamos cómo se hace esto:
Primero despejamos V2 de la Ley de Boyle-Mariotte:
$$V_2=\frac{P_1×V_1}{P_2}$$
Ahora sustituimos el valor de P2 = 2 * P1:
$$V_2=\frac{P_1×10)}{(2×P_2\ )}$$
Cancelamos la cantidad P1 del numerador y del denominador con lo que se obtiene:
$$V_2=\frac{10}{2}$$
De modo que el resultado es: 5 L.
8. Energía cinética y energía potencial
La energía de movimiento que tiene un cuerpo que se conoce como energía cinética (EC), y la energía que tiene almacenada un cuerpo debido a su posición dentro de un sistema. Esta última es conocida como energía potencial (EP). Las expresiones matemáticas para estas cantidades tienen la siguiente forma:
$$EC=\frac{m×v^2}{2}$$
$$EP=m×g×h$$
A partir de estas cantidades, es muy fácil determinar la energía total de un sistema mecánico como la suma de su energía cinética con la energía potencial:
$$Etotal=EC+EP$$
$$EC=(m×v^2)/2+m×g×h$$
Revisa este ejercicio de Física:
Un carrito en la montaña rusa tiene una masa de 100 kg y se encuentra a una alguna de 10 m. ¿Cuál es su energía total si su velocidad es de 1 m/s?
El problema se resuelve fácilmente sustituyendo los valores de las variables proporcionadas:
$$EC=\frac{(100kg)×(1\frac{m}{s})^2}{2}+(100 kg)×(9.8\frac{m}{s})^2)×(10 m)$$
$$Etotal=50\ J+9800J$$
¡Esta energía se conserva a lo largo de toda la trayectoria del carrito!
9. Ley de Coulomb
La Ley de Coulomb proporciona una forma de medir la fuerza que existe entre cargas eléctricas y nos ayuda a comparar los fenómenos eléctricos con la teoría de la mecánica clásica, pues esta ley determina la fuerza que existe entre dos cuerpos debido a su naturaleza eléctrica conforme lo expresa la siguiente formula:
$$F=-KQ\frac{q}{r}^2$$
La constante K es necesaria para hacer la comparación entre cantidades de naturaleza eléctrica y la fuerza que es una cantidad utilizada en mecánica. Dicha constante tiene el valor de 9,000,000 Nm2/C2.
La fórmula expresa que dicha fuerza resulta del producto de las cargas Q y q. Además, expresa que la fuerza disminuye como el cuadrado de r que es la separación que existe entre los centros de las cargas Q y q.
Es importante recordar que la fuerza entra las cargas puede ser positiva o negativa, dependiendo del signo que tengan las cargas. Tampoco olvides que cargas iguales se repelen, mientras que cargas de signo opuesto se atraen. Esta característica está indicada por el signo (-) que precede al factor K en la formula.
Resolvamos el siguiente ejemplo:
Calcula la fuerza que existe entre 2 cargas idénticas Q = q = 0.1 C, y cuya separación es de 30 metros.
Sustituimos en la fórmula de Coulomb y obtenemos:
$$F\ =(-\ (9000000000)Nm^2)((0.1C\times0.1C)/((30m)^2))$$
$$F\ =(-\ (9000000000)Nm^2)(0.1/900\ N)$$
La fuerza de repulsión entre las cargas Q y q es de F = 100,000N.
10. Reflexión y refracción
La reflexión es el cambio de dirección de los rayos de luz que se da en un mismo medio después de tener contacto con la superficie de otro medio. Cuando la superficie del segundo medio es plana entonces ocurre que el ángulo que hace la normal a la superficie con respecto al rayo incidente es igual que el ángulo que subyace entre la normal y la dirección del rayo reflejado.
Esto se expresa en la siguiente ecuación:
$$\theta_i=\theta_r$$
$$n_i\ sin\theta_i=[n_r\ sin][θ_r]$$
Por otro lado, la refracción es el cambio de la dirección de los rayos cuando atraviesan de un medio caracterizado por un índice de refracción a otro medio con índice de refracción nr, en cuyo caso se cumple la siguiente relación entre el ángulo de incidencia y el ángulo refractado (el que hace el rayo transmitido en el segundo medio con la normal a la superficie):
Estudia todas las fórmulas de Física con Unitips
En Unitips, encontrarás una infinidad de temas que te pueden ayudar ya sea para realizar ejercicios, preguntas que pueden venir en tu examen o temas de esta y otras materias.
Recuerda que, además de poner en práctica las fórmulas, también debes entender la teoría, así como conceptos generales sobre Física. Para ello debes tener técnicas que te permitan estudiar de manera efectiva.
No te espantes si ves muchos conceptos o términos que no conoces, al final las herramientas adecuadas y los hábitos de estudio que desarrolles te permitirán aprender mejor.