Módulo de Cálculo diferencial e integral del EXANI-II

Temario y preguntas del módulo específico de Cálculo diferencial

¿Vas a entrar a alguna carrera de ciencias exactas o ingeniería? Quizá te toque presentar el módulo de Cálculo diferencial e integral del EXANI-II. En este blog te explicaremos los temas que necesitas estudiar.

¿Qué temas vienen en el módulo de Cálculo diferencial del EXANI-II?

El Examen Nacional de Ingreso (EXANI-II) es la evaluación más aplicada por las universidades durante el proceso de admisión. Entre sus características, destacan sus contenidos diferenciados según la carrera a la que se quiera ingresar.

En el caso del módulo de Cálculo diferencial e integral, muchas escuelas han decidido establecerlo como requisito para carreras como Matemáticas, Arquitectura, entre otras. Al igual que los otros módulos específicos, éste se compone de 24 reactivos, divididos en dos secciones. El temario completo es el siguiente:

• Cálculo diferencial
  • Límites
    • Propiedades de los límites
    • Límites de funciones polinominales y con variables independientes
  • La derivada
    • Derivadas por definición, de funciones trigonométricas, de funciones exponenciales y logarítmicas y de funciones polinominales
    • Recta tangente de funciones algebraicas
  • Aplicaciones de la derivada
    • Aplicaciones físicas de la derivada (velocidad instantánea, distancia, rapidez de cambio y de optimización)
  • Cálculo integral
    • La integral
      • Partición de funciones
      • Manipulación algebraica y aritmética
      • Propiedades de la integral
    • Métodos de integración
    • Aplicaciones de la integral definida
      • Problemas de área, volumen y movimiento con integrales definidas

No olvides que, además de estos temas, también te encontrarás la sección de áreas transversales, que abarca temas de habilidades y conocimientos generales y equivale al 50% del examen, por lo que será necesario que también te dediques a practicar y estudiar estos temas.

Uno de los primeros pasos que puedes dar para pasar el EXANI-II es responder un examen diagnóstico. Éste te ayudará a medir tu nivel académico y a conocer en qué materias debes poner más empeño. Regístrate en el siguiente enlace y recibe uno completamente gratis.

{{cta('b897ab87-3cdd-46b7-81fa-dc56af30366a','justifycenter')}}

Reactivos del EXANI-II: módulo de Cálculo diferencial

Si todavía no conoces el tipo de preguntas que vendrán en el EXANI-II, revisar las preguntas del módulo de Calculo diferencial te ayudará a dar el primer paso y familiarizarte más con éstas. Cada una viene con retroalimentación, pero es recomendable que intentes responderlas primero por tu cuenta.

Si además de reactivos tipo examen, quieres acceder también a lecciones y clases que te expliquen de manera dinámica todos los temas de tu examen, regístrate en el siguiente enlace y accede a la plataforma Unitips de preparación para el examen Ceneval sin costo.

{{cta('f0874e35-fdd7-486d-bcf0-d2b1ffb333b8')}}

Cálculo diferencial

1. Método por el cual se resuelve un límite indeterminado que, al sustituir la variable y otras expresiones algebraicas, el resultado es 0/0.

1. Factorización
2. Igualación
3. Eliminación

Igualación y eliminación son métodos para resolver sistemas de ecuaciones, mas no límites. Si intentamos resolver un límite sustituyendo las x por el valor al que tiende el límite y se obtiene un resultado indeterminado, se pueden factorizar las expresiones del numerador o del denominador para eliminar la parte indeterminada del resultado, veamos un ejemplo.

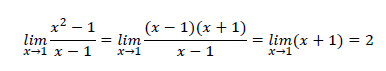
Este método se llama factorización, por lo que la respuesta correcta es el inciso a).

2. Calcula el siguiente límite:

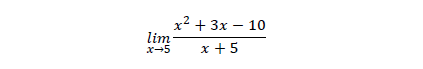
1. -7
2. 3
3. 7

La manera más rápida de resolver un límite es sustituir en la función el valor al que tiende la variable:

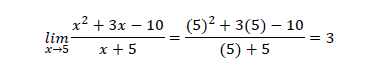
Como el resultado de la sustitución no es un número indeterminado del tipo 0/0, no es necesario hacer nada más, la respuesta correcta es el inciso b).

3. Resuelve por sustitución el siguiente límite:

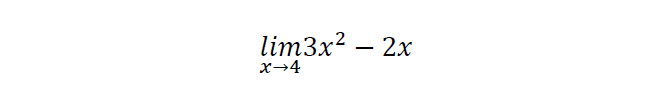
1. 56
2. 0
3. 40

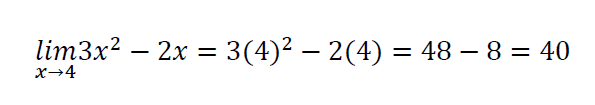La respuesta correcta es el inciso c).

4. Es el valor que toma la derivada de una función en un punto mínimo de la función original.

1. 1
2. 0
3. -1

La derivada indica el valor de la pendiente de la recta tangente en un punto cualquiera de la curva de la función, el signo de esta pendiente nos indica si la función es creciente o decreciente.

En los puntos mínimos y máximos, la recta tangente tiene una pendiente igual a 0 porque son puntos en los que la función cambia de comportamiento creciente a decreciente (máximos) o viceversa (mínimos). La respuesta correcta es el inciso b).

5. Selecciona las opciones correctas:

Si la derivada de una fusión f(x) es 0 al evaluarla en un punto x₀ entonces…

1. f(x₀) es un mínimo
2. f(x₀) es un máximo
3. f(x) es una constante
4. f(x) es una tangente
5. f(x₀) es una tangente
6. f(x) es una pendiente

a) 1, 2, 3

b) 2, 4, 6

c) 1, 4, 5

Si la derivada de una función es cero, la función será constante sin importar el punto en el que la evaluemos. Por otro lado, una función forma máximos y mínimos en los puntos en donde la derivada es cero.

Si en todos los valores de x la derivada es cero, todos los puntos pertenecientes a la función son máximos y mínimos, esto únicamente puede ser cierto en una función constante, es decir, una que forma una recta horizontal debido a que el valor de la función es fijo y no cambia al modificar a la variable. La opción correcta es el inciso a).

Cálculo integral

6. La integral de una recta horizontal a cierta altura con los límites de integración de 0 a b nos da el:

1. área de un rectángulo
2. perímetro de un rectángulo
3. área de un círculo

Una integral definida nos da el tamaño del área bajo la curva de la función. Si la función es una recta horizontal, el área bajo la curva corresponderá a un rectángulo. La respuesta correcta es el inciso a).

7. Elige el cambio de variable que debemos usar para calcular la integral de la siguiente función:

$$f(x)=2xcos(x^2)$$

1. x², 2xdx
2. x, dx
3. cos (x), sin (x)dx

Para poder resolver una integral con el método de cambio de variable es necesario que la derivada de la función compuesta se encuentre en la función.

En este ejemplo, x² que se encuentra como argumento en el coseno tiene a su derivada (2x) en la misma función, hacer un cambio de variable vuelve a la integral mucho más fácil de resolver.

Para resolver la integral debemos cambiar a x² por u y a 2xdx por du. La respuesta correcta es el inciso a).

8. Encuentra el área bajo la curva de la siguiente función, considerando que s encuentra delimitada por el eje y la recta x=2.

$$ f(x)=(x+1)(x-1)$$

1. ⅔
2. -⅔
3. 3

Encontrar el área bajo la curva implica resolver una integral definida desde x=0 hasta x=2:

$$\int_{0}^{2}{(x+1)(x-1)dx}$$

Si multiplicamos los binomios conjugados, obtenemos una diferencia de cuadrados, de modo que facilita a la resolución de la integral.

$$\int_{0}^{2}{{(x}^2-1)dx}$$

$$\int_{0}^{2}{x^2dx}-\int_{0}^{2}1dx$$

$$\left[\frac{x^3}{3}-x\right]_0^2=\left[\frac{(2)^3}{3}-2\right]-\left[\frac{(0)^3}{3}-0\right]=\frac{8}{3}-2=\frac{2}{3}$$

La respuesta correcta es el inciso a).

En caso de que necesites acceder a más preguntas de este módulo y de otros temas que aparecerán en tu examen, busca simuladores del EXANI-II, que también te ayudarán a tener un puntaje aproximado del que obtendrías el día de la aplicación.

Curso, guía y exámenes para el módulo de Cálculo diferencial

Aunque estas preguntas pueden ser útiles para comenzar a estudiar temas específicos para el ingreso a tu carrera, es importante que utilices otros recursos además de la información del módulo de Cálculo diferencial del EXANI-II.

Es recomendable que encuentres técnicas de estudio que se adapten a tu estilo de aprendizaje y te ayuden a comprender y practicar aquellas materias que te resulten más difíciles. Utilizar herramientas personalizadas puede ser de gran ayuda para estudiar de manera más efectiva.

En el curso de Unitips, encontrarás una plataforma en línea completamente adaptable a tus necesidades de aprendizaje. Todos los temas están explicados a través de lecciones dinámicas y sencillas, permitiéndote aprovechar tu tiempo de manera eficiente. Si quieres probarlo, regístrate en el siguiente enlace y accede a la versión gratuita.

«Regístrate sin costo y recibe tres clases gratuitas del curso mejor calificado de Google. Empieza aquí.»