La ecuación de la elipse
La elipse es el lugar geométrico de los puntos del plano de tal manera que la suma de las distancias a dos puntos llamados focos, es constante. Si estás interesado en próximamente presentar tu examen de ingreso a la UAM, éste blog es para ti.
Unitips te ayuda con el tema de “La Elipse” para que en tu examen de ingreso a la UAM puedas contestar de manera sencilla y con seguridad.
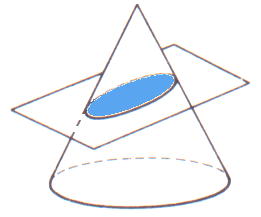
Ahora bien, es importante que sepas que la elipse nace al cortar un cono con un plano de manera inclinada, y que además, tiene ciertos elementos y ecuaciones que debes dominar para presentar tu examen de ingreso a la UAM.
Como elementos tiene:
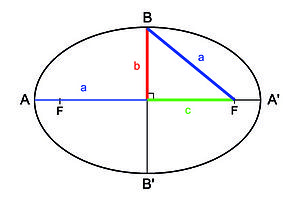
Un centro -> C(h,k)
Dos vértices -> La distancia de un vértice a otro se le llama Eje Mayor
$$\bar{V_{1}V_{2}}=2a$$
Dos extremos -> La distancia de un extremo a otro se le llama Eje Menor
$$\bar{B_{1}B_{2}}=2b$$
Dos focos -> La distancia de un foco a otro se le llama Eje Focal
$$\bar{F_{1}F_{2}}=2c$$
Una condición, donde dice que a>b y a>c $$a^{2}=b^{2}+c^{2}$$
Un lado recto que se obtiene como
$$LR=\frac{2b^{2}}{a}$$
La excentricidad debe de ser menor a cero,
$$e=\frac{c}{a}<0$$
Te recomendamos que para identificar en tu examen de ingreso a la UAM, si una elipse es horizontal o vertical, te fijes en la ecuación ordinaria en el número más grande (que es “a”, se sabe de la condición).
ELIPSE VERTICAL
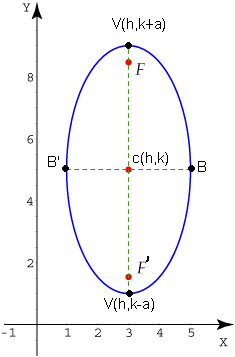
Centro: C(h,k)
Vértices:
$$V(h,k\pm a)$$
Extremos:
$$B(h\pm b,k)$$
Focos:
$$F(h,k\pm c)$$
Ecuación ordinaria de la elipse vertical:
$$\frac{(x-h)^{2}}{b^{2}}+\frac{(y-k)^{2}}{a^{2}}=1$$
Ecuación General de la Elipse
Es de la forma:
$$Ax^{2}+Cy^{2}+Dx+Ey+F=0$$
donde A y C deben de ser diferentes pero con mismos signos.
A continuación se mostrará un ejemplo para que en tu examen de ingreso a la UAM seas acertivo con tus respuestas.
Encuentra la ecuación general de la elipse con centro en C(-2,4), un vértice en (-2,8) y con foco en (-2,6).
Primero:
Identificamos qué tipo de elipse es, en este caso, es una elipse vertical (porque la coordenada x=-2 queda fija en los datos del vértice y del foco), además, del centro que es (-2,4), deducimos que h=-2 y k=4.
Sabiendo que es vertical, comparamos
$$V(h,k\pm a)$$
con (-2,8), entonces decimos que h=-2 y que k+a=8. Se sustituyen los valores que ya se conocen, que es k=4.
Entonces, 4+a=8. Despejando el valor de “a” queda que es igual a 4 (a=4).
Ahora, comparamos
$$F(h,k\pm c)$$
con (-2,6), entonces decimos que h=-2 y que k+c=6. Se sustituyen los valores que ya se conocen, que es k=4.
Entonces, 4+c=6. Despejando el valor de “c” queda ue es igual a 2 (c=2).
Segundo:
Para poder sustituir en la ecuación ordinaria de la elipse vertical, se tiene que saber los valores de “h”, “k”, “a” y “b”. Aquí, solo falta saber el valor de “b”.
Entonces, utilizamos la condición de la elipse, que dice que $$a^{2}=b^{2}+c^{2}$$
Se despeja a b y se sustituye:
$$b^{2}=a^{2}-c^{2} -> b^{2}=16-4=12$$
Tercero:
Se sustituye en la ecuación ordinaria de la elipse vertical y se realizan las operaciones respectivas hasta igualar a cero con “x” positiva:
$$\frac{(x-h)^{2}}{b^{2}}+\frac{(y-k)^{2}}{a^{2}}=1$$
$$\frac{(x+2)^{2}}{12}+\frac{(y-4)^{2}}{16}=1$$
$$\frac{4(x+2)^{2}+3(y-4)^{2}}{48}=1$$
$$4(x^{2}+4x+4)+3(y^{2}-8y+16)=48$$
$$4x^{2}+16x+16+3y^{2}-24y+48-48=0$$
$$4x^{2}+3y^{2}+16x-24y+16=0$$
Para poder entender mejor este tema para tu examen de ingreso a la UAM, práctica con más ejercicios. Unitips te recomienda la sección de blogs en la página oficial, ahí podrás encontrar diversos temas de Matemáticas, de Biología, de Historia, de Razonamiento Verbal, entre otros, que seguramente te funcionarán para tu examen de ingreso a la UAM. Y no te olvides de descargar la guía de repaso express para que te prepares desde ahora.




