¿Cómo usar la fórmula chicharronera?

Aprende a utilizar la fórmula chicharronera

Si te encuentras estudiando para tu examen de admisión a la universidad o estás repasando temas importantes de la materia de matemáticas, seguramente ya descubriste que la fórmula chicharronera es una herramienta muy útil.

Para ayudarte en este proceso, en este artículo te explicamos paso a paso en qué consiste esta fórmula, cómo usarla y ejercicios resueltos que te ayudarán a comprenderla mejor.

¿Para qué sirve la fórmula chicharronera?

La fórmula chicharronera o fórmula general es una expresión que te ayudará a encontrar la solución de ecuaciones de segundo grado.

Estas ecuaciones, también llamadas ecuaciones cuadráticas, son un polinomio compuesto por tres elementos: un coeficiente cuadrático, un coeficiente lineal y un término independiente. Su representación es la siguiente:

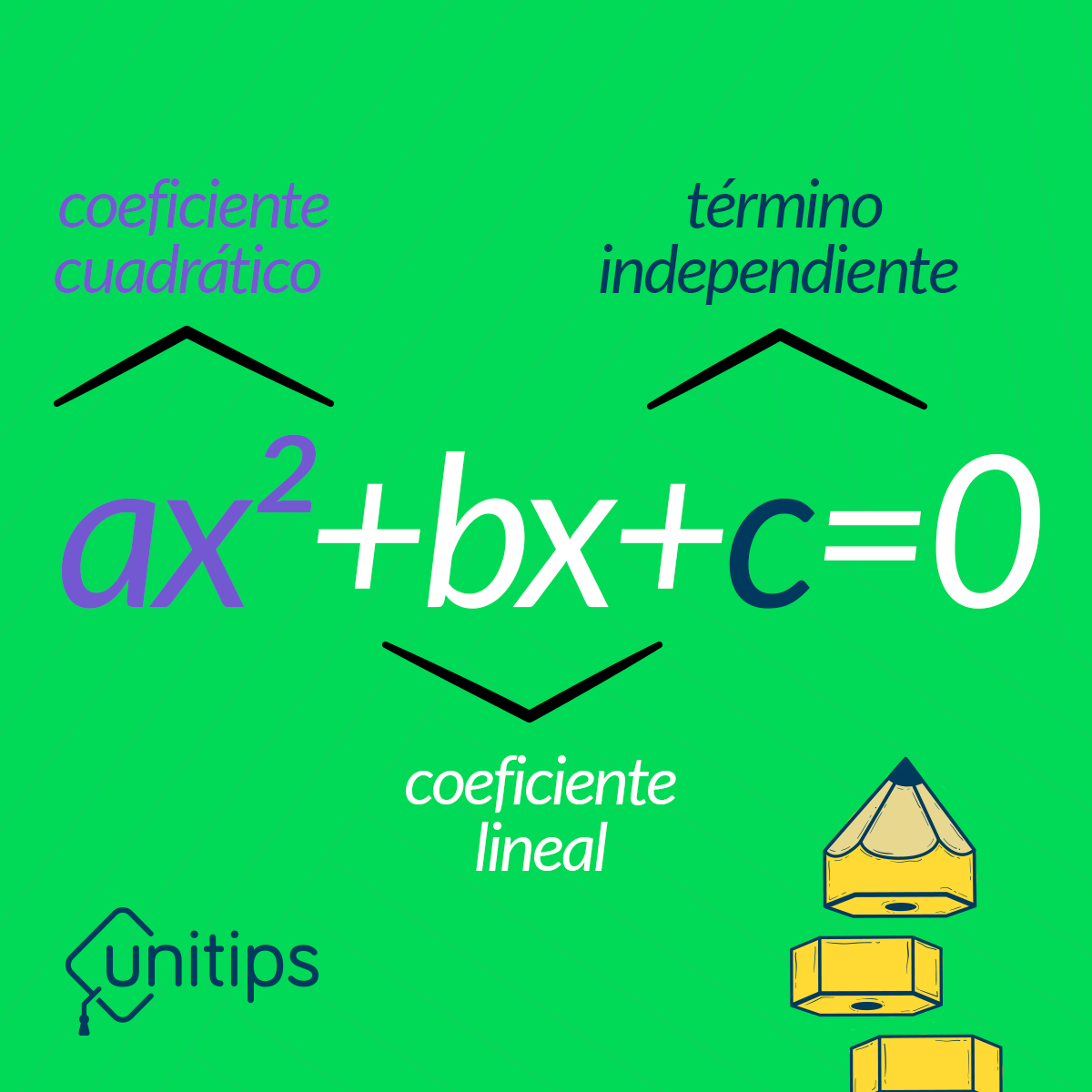
A través de reemplazar cada término de la ecuación en la fórmula, esta se puede utilizar para encontrar la solución o soluciones que esta tenga. La fórmula se representa de la siguiente manera:

A continuación, te explicaremos paso a paso cómo aplicar la fórmula chicharronera y encontrar la solución de las ecuaciones de segundo grado. Mientras tanto, te invitamos a registrarte a la prueba gratuita del curso Unitips, donde encontrarás ejercicios y videos animados donde te explicarán este y otros temas de tu guía de ingreso a la universidad.

Pasos de la fórmula chicharronera

Utilizar la fórmula chicharronera es muy sencillo, sin embargo, es importante que prestes atención a cada paso que te explicaremos. Para que resulte más sencillo, resolveremos un ejemplo de ecuación cuadrática con este método.

Paso 1. Ubica los elementos de la fórmula

En primer lugar, es necesario que ubiquemos los tres elementos de la ecuación de segundo grado. Esto nos ayudará a colocarlas correctamente en la fórmula. Revisemos el siguiente ejemplo:

$$3x^2-11x-4=0$$

En este caso, los elementos son:

• a = 3
• b =  ̶ 11
• c =  ̶ 4

Paso 2. Reemplaza los términos en la fórmula general

Una vez que hayas ubicado los términos de la ecuación cuadrática, colócalos en la fórmula chicharronera. Respeta los signos de cada término.

$$x=\frac{-11\pm\sqrt{-11^2-4(3\times-4)}}{2(3)}$$

Paso 3. Resuelve las operaciones

Ahora que tienes cada elemento en el lugar indicado por la fórmula general, es momento de que resuelvas las operaciones para obtener x. Toma en cuenta las leyes de los signos mientras realizas esto. Te sugerimos que lo realices por pasos, iniciando por las operaciones dentro de la raíz cuadrada:

1.

$$x=\frac{(11\pm\sqrt(121-4(-12)))}{6}$$

2. 

$$x=\frac{(11\pm\sqrt(121+48))}{6}$$

Al ser   ̶12 un número negativo, multiplicado por otro negativo, modifica la resta que teníamos en la fórmula original y la convierte en una suma.

3.

$$x=\frac{(11\pm\sqrt169)}{6}$$

4.

$$x=\frac{(11\pm13)}{6}$$

5. Este paso es muy importante ya que, debido al ± de la fórmula, obtendremos dos resultados, que llamaremos x₁ y x₂.

Primero, conseguiremos el valor de x₁ utilizando el valor positivo:

$$x=\frac{(11+13)}{6}$$

$$x=\frac{24/}{6}$$

$$x=4$$

Ahora, para obtener x₂, realizaremos la misma operación, pero con el valor negativo de la fórmula:

$$x=\frac{11-13)}{6}$$

$$x=\frac{-2}{6}$$

$$x=\frac{1}{3}$$

Ejercicios de la fórmula chicharronera

Para usar la fórmula general, es necesario que sepas que no habrá dos soluciones para todas las ecuaciones de 2° grado, como en el ejemplo anterior, sino que esto depende del valor de la discriminante que en este caso es b² ̶ 4ac, de modo que:

• Si este es mayor a cero, obtendrás dos soluciones.
• Si es igual a cero, sólo obtendrás una solución.
• Si es menor a cero, el resultado será una raíz negativa, es decir, un número no real.

En el ejemplo anterior, tuvimos el primer caso ya que, al ser b² ̶ 4ac = 169, se consiguieron dos soluciones. Veamos ejemplos de los otros casos.

Ejemplo 1. Resolvamos la siguiente ecuación por medio de la fórmula chicharronera:

$$x^2+4x+4=0$$

1. Ubica los elementos de la ecuación:

• a = 1
• b = 4
• c = 4

2. Colócalos en la posición que le corresponde dentro de la fórmula general:

$$x=\frac{-4\pm\sqrt{4^2-4(1\times4)}}{2(1)}$$

3. Comienza por resolver la discriminante de la ecuación:

$$x=\frac{-4\pm\sqrt{4^2-4(4)}}{2(1)}$$

$$x=\frac{-4\pm\sqrt{16-16}}{2(1)}$$

$$x=\frac{-4\pm\sqrt0}{2(1)}$$

4. Como ves, el valor es igual a 0, por lo tanto, sólo obtendrás una solución.

$$x=-\frac{4}{2}$$

$$x=-2$$

Resolver en primer lugar la operación dentro de la raíz cuadrada te ayudará a predecir si tendrás una, dos o ninguna solución. Veamos el último ejemplo:

$${-x}^2+4x-7=0$$

1. Identificamos los valores correspondientes:

• a = -1
• b = 4
• c = -7

Una vez ubicados en su valor dentro de la fórmula, se resuelve primero las operaciones de la discriminante.

$$x=\frac{-4\pm\sqrt{4^2-4((-1)(-7))}}{2(1)}$$

$$x=\frac{-4\pm\sqrt{16-28}}{2(1)}$$

$$x=\frac{-4\pm\sqrt{-12}}{2(1)}$$

Debido a que las raíces de los números negativos no forman parte del conjunto de números reales, por lo tanto, esta ecuación no tiene soluciones reales.

¿Te pareció útil la información de este artículo? Utiliza el examen diagnóstico que te dejamos a continuación para poner a prueba tus conocimientos en esta y en otras materias. 

Si ya estás estudiando con alguno de los cursos de ingreso a la universidad de Unitips, no olvides compartir tu código Unicash con tus compañeros y amigos para que reciban increíbles descuentos y tú puedas acumular puntos en nuestro sistema de recompensas.

Pero, en caso de que apenas nos estés conociendo, te invitamos a que te registres en nuestra plataforma sin costo y accedas a recursos como lecciones animadas, preguntas tipo examen, clases en vivo, entre otros, que te ayudarán a aumentar tus posibilidades de ingreso a la escuela que quieres.

«Los Unitipers tienen hasta 5 veces más posibilidades de ingresar a la universidad en su primer intento. Forma parte de nuestra comunidad y alcanza tus metas ya.»