---
title: "Física: Tiro parabólico Guía de temas para tu examen de la UNAM"
description: Aprende Física para tu examen de la UNAM con el Super Bowl.
image: https://blog.unitips.mx/hubfs/Content/Redise%C3%B1o/Open%20Graph_default/Generico_B.jpg
---
Cursos
[UNAM](https://www.unitips.mx/cursos-admision/guia-unam-mx/) [IPN](https://www.unitips.mx/cursos-admision/guia-ipn/) [UAM](https://www.unitips.mx/cursos-admision/guia-uam/) [EXANI-II](https://www.unitips.mx/cursos-admision/guia-exani-ii/) [BUAP NUEVO](https://www.unitips.mx/cursos-admision/guia-buap-epiu/) [COLLEGE BOARD PAA](https://www.unitips.mx/cursos-admision/guia-college-board-paa/) [EXHCOBA](https://www.unitips.mx/cursos-admision/guia-exhcoba/) [ECOEMS](https://www.unitips.mx/cursos-admision/guia-bachilleratos-unam-ipn/) [EXANI-I](https://www.unitips.mx/cursos-admision/guia-exani-i/)
---
[Todos los cursos](https://www.unitips.mx/cursos-admision/)
[Planes](https://www.unitips.mx/planes-y-precios/) [Blog](https://blog.unitips.mx) [Contacto](https://www.unitips.mx/contacto/) [Reseñas](https://www.unitips.mx/nosotros/testimoniales/)
[Inicia Sesión](https://www.unitips.mx/accounts/login/) [Regístrate](https://www.unitips.mx/accounts/signup/)
 abril 15
Preparación
# Física: Tiro parabólico Guía de temas para tu examen de la UNAM
## **En Unitips preparamos este blog para ayudarte a entender la cinemática.**
La cinemática es una rama de la [física](https://www.unitips.mx/blog/contenido-de-examen-unam-las-leyes-de-newton/) que estudia el movimiento de los cuerpos, sin tomar en cuenta las causas que originaron dicho movimiento. Este es un tema muy común en el [*examen* de *admisión*](https://blog.unitips.mx/examen-unam-que-preguntan-para-area-1)*[a la UNAM](https://blog.unitips.mx/examen-unam-que-preguntan-para-area-1)*, debido a que es uno de los primeros que se estudian en la mecánica clásica, y como seguro ya estás estudiando para tu *examen.*
En la cinemática no importa qué fuerzas originaron el movimiento; por lo tanto, para estudiar el tiro parabólico sólo se necesitan unos cuantos datos para resolver problemas relacionados con este tema y que mejor que hacerlo, considerando una jugada de americano, pues aunque no lo creas, el Super Bowl, se presta para aprender muchísimas cosas de Física.
[](https://cta-redirect.hubspot.com/cta/redirect/3888270/1ac56a2a-c8bb-449c-a639-05a7832e7b09)
**El siguiente problema es similar a los que podrían venir en el *examen* de *admisión* de la UNAM.**
**Problema:** Si un jugador de fútbol americano lanza un balón con una velocidad inicial $$ $$ de 60 km/h con un ángulo $$( \\theta )$$ de 40°, ¿cuál será la distancia recorrida por el balón y cuál será la altura máxima?
Primero recordemos que para resolver problemas de cinemática se utiliza la ecuación de movimiento, debes tener en cuenta que este cuerpo se mueve en la dirección “x” y en la dirección “y”:
- Ec. de movimiento en “x”: $$x=\\frac{1}{2}\\cdot a\\cdot t^{2}+v\_{0}\\cdot cos\\Theta \\cdot t+x\_{0}$$
- Ec. de movimiento en “y”: $$y=-\\frac{1}{2}\\cdot g\\cdot t^{2}+v\_{0}\\cdot sen\\Theta \\cdot t+y\_{0}$$
[](https://cta-redirect.hubspot.com/cta/redirect/3888270/932052a6-7bc5-4553-b1ad-77c5e15bea15)
En el movimiento parabólico el movimiento en el eje “x” es constante, por lo que no hay aceleración. Además debe considerarse para cada ecuación el componente del vector de la velocidad en el eje “x” y en el eje “y”.
En el eje “y” la aceleración es igual a la gravedad. A partir de estas dos ecuaciones se pueden deducir las siguientes, las cuales nos ayudan a hacer el cálculo más directo durante el *examen*:
- Altura máxima: hmax = $$h\_{max}= \\frac{\\left (v\_{0}\\cdot sen\\Theta \\right )^{2} }{2\\cdot g}$$
- Alcance horizontal: x = $$\\Delta x=v\_{0}^{2}\\cdot \\frac{sen\\left ( 2\\Theta \\right )}{g}$$
El siguiente paso es sustituir los valores dados en el problema en las ecuaciones, recuerda utilizarlos en unidades del sistema internacional, a menos que en el *examen t*e pidan otras unidades:
- 60 km/h (1000m/1km)(1h/3600s) = 16.6666 m/s
- hmax = 5.85 m
- Alcance horizontal: Δx = 27.885 m
Como te podrás dar cuenta, sólo bastaron dos datos para poder hacer los cálculos necesarios. En el examen de la UNAM podrían preguntarte el tiempo, por lo cual también te damos esa ecuación, sólo por si acaso:
- Tiempo: $$t=2\\frac{v\_{0}\\cdot sen\\Theta }{g}$$
### **Fórmulas:**
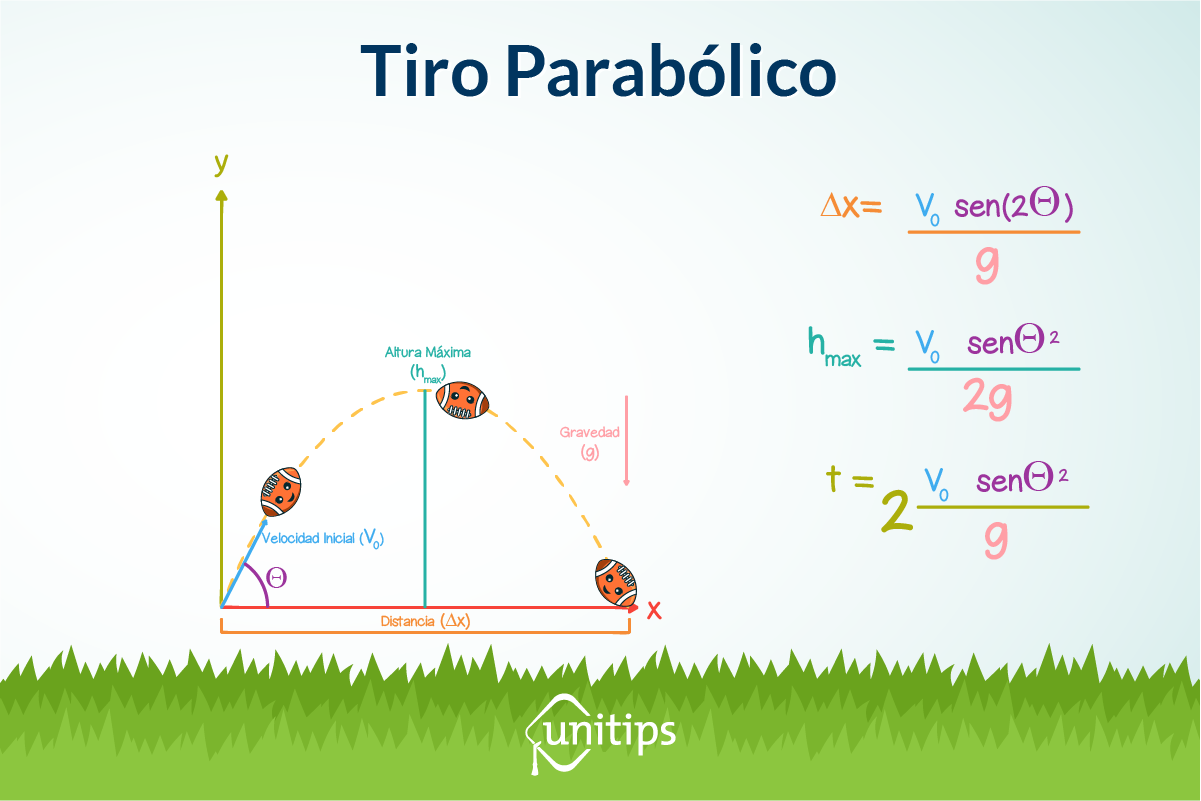Recuerda que el *examen de admisión de la UNAM* está cada vez más cerca.
## Otros Artículos que te podrían interesar
[](https://blog.unitips.mx/todo-lo-que-necesitas-saber-del-suayed)
Elecciónoctubre 6
### [Convocatoria UNAM SUAyED 2026: fechas, registro y carreras](https://blog.unitips.mx/todo-lo-que-necesitas-saber-del-suayed)
La convocatoria UNAM SUAyED de noviembre de 2026 ya se publicó. El registro estará abierto del 8 al 12 de octubre y el examen será presencial, del 18 al 22 de ...
[Leer PublicaciónVer más](https://blog.unitips.mx/todo-lo-que-necesitas-saber-del-suayed)
[](https://blog.unitips.mx/convocatoria-uam)
Admisionesoctubre 5
### [Convocatoria UAM 2026: tercera vuelta, registro y examen presencial](https://blog.unitips.mx/convocatoria-uam)
La tercera convocatoria UAM 2026 ya se publicó. El registro será del 5 al 11 de octubre para ingresar en invierno de 2027. Esta vez, el examen será presencial. ...
[Leer PublicaciónVer más](https://blog.unitips.mx/convocatoria-uam)
[](https://blog.unitips.mx/como-entrar-a-la-unam)
Admisionesoctubre 1
### [¿Cómo entrar a la UNAM en 2027?](https://blog.unitips.mx/como-entrar-a-la-unam)
¿Cómo ingresar a la UNAM en 2027? ¿Ya decidiste que quieres continuar tus estudios en la UNAM, pero no sabes qué hacer para lograrlo? Lo entendemos, entrar a ...
[Leer PublicaciónVer más](https://blog.unitips.mx/como-entrar-a-la-unam)
[](https://blog.unitips.mx/hs/cta/wi/redirect?encryptedPayload=AVxigLKSAglWsM5APPFymFnaFHHQbo2kiyFOBE%2FjuaCDDWp%2FaYe2cVcxa0xjwdYTLNd2%2FmCHPSN%2Fd%2BApjsYvnufbwTHioHyOmimjK23GpfD4oe%2FMNyylpK7iCrg68fF07UxX4V3LyFh5M6FzU43BjFGaV4kftWIt2rFxVIPtPmrmsJEF2XHuyhsD%2Bz5pwIotiyPXbPSiZhIaX%2FqqiCGJTzY%3D&webInteractiveContentId=223769905843&portalId=3888270)
[](https://blog.unitips.mx/hs/cta/wi/redirect?encryptedPayload=AVxigLK%2Bd8gUd%2Fqk1Qs2dBZencsf%2Fh4jIwb7lToGg9kJuAQqsyk2cRdyFIQNzhBCV2NimU5OPI%2BHbQUNGKscxhBlE3ERX3yEh6Nszd%2FlyyVA8yQiTzNcu9GrRlJhH8IpMETJ0Xf5Zvhy7OnJKAd4w1bTn14on4bCi46pkJREphE2KFF%2B%2FVKku6nf%2FsK%2BXuEPMk7T3cdmLLUrrpHYA0SZbLw%3D&webInteractiveContentId=223769850183&portalId=3888270)
×
## Empieza gratis hoy mismo
Sin tarjeta de crédito. Cancela cuando quieras.
[Pruébalo Gratis](https://www.unitips.mx/accounts/signup/)
## Cursos
- [UNAM](https://www.unitips.mx/cursos-admision/guia-unam-mx/)
- [IPN](https://www.unitips.mx/cursos-admision/guia-ipn/)
- [UAM](https://www.unitips.mx/cursos-admision/guia-uam/)
- [EXANI-II](https://www.unitips.mx/cursos-admision/guia-exani-ii/)
- [BUAP NUEVO](https://www.unitips.mx/cursos-admision/guia-buap-epiu/)
- [COLLEGE BOARD PAA](https://www.unitips.mx/cursos-admision/guia-college-board-paa/)
- [EXHCOBA](https://www.unitips.mx/cursos-admision/guia-exhcoba/)
- [ECOEMS](https://www.unitips.mx/cursos-admision/guia-bachilleratos-unam-ipn/)
- [EXANI-I](https://www.unitips.mx/cursos-admision/guia-exani-i/)
## Empresa
- [Unitips](https://www.unitips.mx/)
- [Blog](https://blog.unitips.mx)
- [Contacto](https://www.unitips.mx/contacto/)
- [Términos y condiciones](https://www.unitips.mx/legal/terminos-y-condiciones/)
- [Aviso de privacidad](https://www.unitips.mx/legal/aviso-de-privacidad/)
En Unitips queremos que estés contento, así que recuerda que puedes probar el curso completamente gratis
© 2026 UNITIPS SAPI de CV [Aviso de privacidad](https://www.unitips.mx/legal/aviso-de-privacidad/) y [Términos y condiciones de uso](https://www.unitips.mx/legal/terminos-y-condiciones/) [mailto:soporte@unitips.mx](mailto:soporte@unitips.mx)
UNAM, CENEVAL, UAM, IPN, ECOEMS, BUAP, EXHCOBA y College Board son marcas e instituciones no vinculadas a Unitips. Este sitio no está aprobado, patrocinado ni afiliado a ellas. Unitips no garantiza el ingreso ni una similitud absoluta de contenidos con los exámenes oficiales. Los materiales pueden actualizarse conforme cambien los temarios o lineamientos de cada institución. Al utilizar este sitio, aceptas nuestro [Aviso de Privacidad](https://www.unitips.mx/legal/aviso-de-privacidad/) y los [Términos y Condiciones de Uso](https://www.unitips.mx/legal/terminos-y-condiciones/).